3.5: Thermal Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Work Between Colliding Objects
In the previous section we introduced the term thermal energy. We used this phrase as a catch-all to describe the form that energy takes when non-conservative forces internal to the system do work. It was not clear at that time why we had to introduce this element to our model, so let's examine it closer here.
When we first introduced the idea of a system, it was mentioned that while internal forces all come in third law pairs, the work done by these pairs are not generally equal-and-opposite. Applying this fact to a non-conservative force like friction is particularly enlightening. Consider the following physical situation: A book slides off a frictionless horizontal ledge directly onto another book which is at rest on a frictionless horizontal surface. There is a kinetic friction force between the two books, and they rub against each other until they are both moving along together at the same speed (see Figure 3.5.1 below).
Figure 3.5.1 – No "Equal-and-Opposite" Law for Work
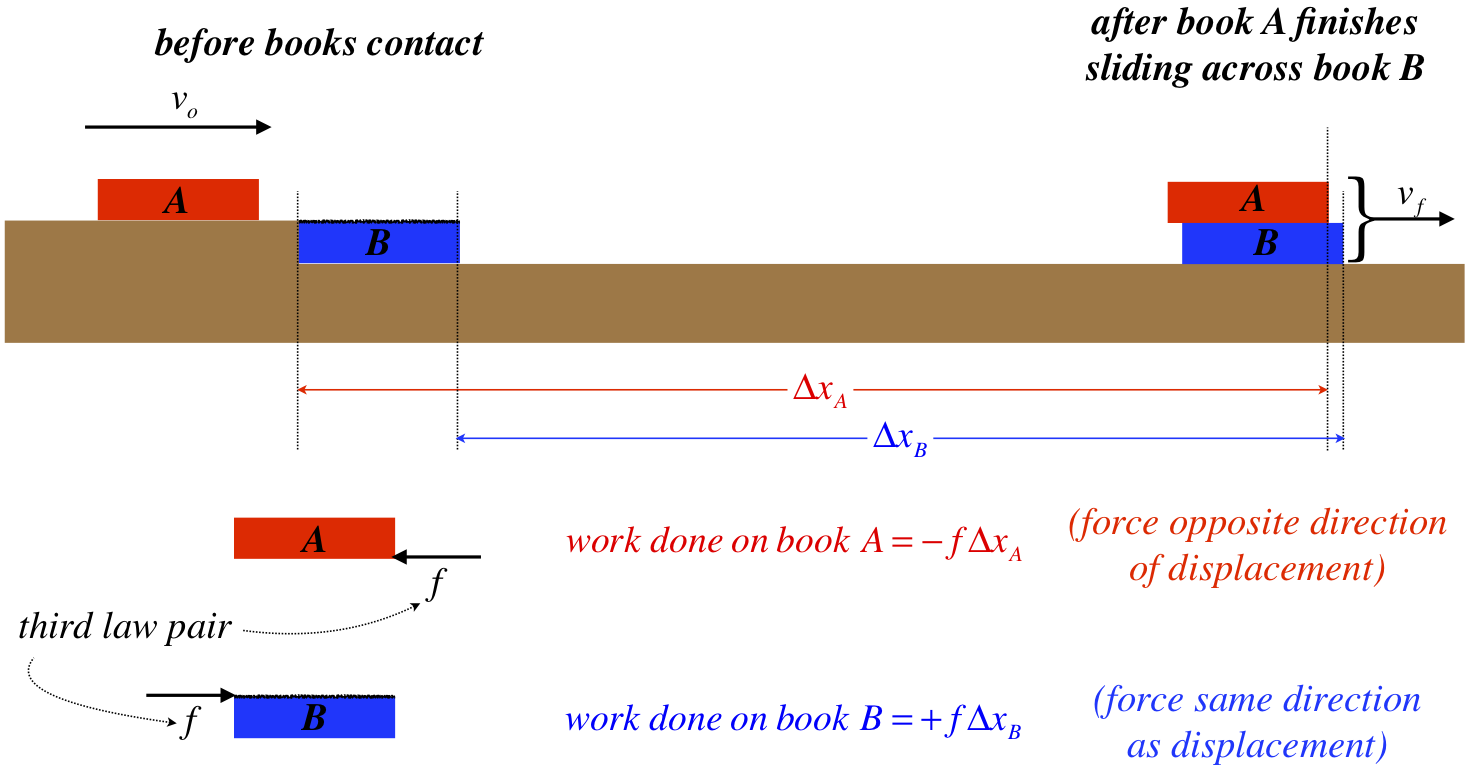
Newton's third law assures that both books experience equal friction forces in opposite directions, but the work done by the friction force on book A is greater (in magnitude) than the work done on book B, because the displacement is greater. The friction force opposes the displacement of book A, so negative work is done on that book, while positive work is done on book B. Remember that we are interested in the overall effect of internal forces on the system, which in this case is the two books. We see that in fact in this case there is a net negative work done on the system:
workdoneonsystem=−fΔxA+fΔxB=−f⋅(ΔxA−ΔxB)=−f⋅(distancetopbookslidesacrossbottombook)
This is an isolated system, which means that the negative work calculated above is not coming from outside. Our conservation models require that the total energy of an isolated system doesn't go up or down, though it can change form. The kinetic energy of this system drops as a result of the books coming in contact (this may not be clear at this point, but we will see this is true in the next chapter, so for now let's just accept it as true), and the energy can't go into potential energy, since the kinetic friction force is non-conservative. We put this energy conversion into the third type of energy in our model – thermal energy – and it is precisely equal to the (negative of the) work computed from the friction force acting through the rubbing distance.
It should also be noted that this analysis is not exclusive to kinetic friction. We would get the same result if the two books compressed a spring, provided we take as the "after" time the moment when the spring is completely compressed. In that case, the magnitude of the work done by the spring force on one book is not equal to the work done by the spring force on the other, but the difference in work (which is again negative) is stored in the potential energy of the spring.
Microscopic Model
While we will be staying with our macroscopic model of interactions, it helps with our understanding of thermal energy to consider a model of what is happening on smaller scales. We know that a macroscopic amount of matter is comprised of trillions upon trillions of atoms. If this collection of matter is a gas, then the particles don't interact very much with each other, while they do interact (with electromagnetic forces) if the particles make up a liquid or solid. Regardless of the forces acting between them, the particles are able to move, which means that they possess kinetic energy. If they interact electromagnetically, then the presence of this conservative fundamental force means that the particles also possess some potential energy.
So what happens when a system gains thermal energy, like when kinetic friction does net-negative work on the system, as in our example above? This energy is conveyed from the macroscopic to the microscopic modes of kinetic and potential energy. In other words, the energy doesn't mysteriously disappear from the universe, it just disappears from our macroscopic model, and can only truly be taken into account with a microscopic model. But there is something very subtle and fundamental that is going on at the same time.
If the energy that was macroscopically-mechanical (e.g. the kinetic energy of book A before it reaches book B in the example above) simply changes into energy that is microscopically-mechanical (kinetic and potential energy of the atoms in both books), then why refer to thermal energy as being fundamentally different from mechanical energy in our macroscopic model? The reason has to do with the one-way nature of the energy transfer into thermal. The kinetic and potential energies of the atoms are randomly-distributed and randomly-oriented. With the atoms vibrating in random directions (they vibrate because molecular bonds create restoring forces similar to tiny springs), all completely out-of-sync, then to give the kinetic energy back to the macroscopic realm, these trillions of particles would have to somehow coordinate their motions. The probability of the random motions of all the atoms being in the same direction at the same time – which is what needs to happen for the macroscopic object to move faster and get back its kinetic energy – is vanishingly small.
So for our macroscopic model, we separate the kinetic and potential energies that apply to large objects (mechanical energy) from those that apply to their randomly-moving atomic constituents (thermal energy). Both are energy, so both measure the same physical property, but conversions of mechanical energy into thermal energy are a one-way street – it's easy to disorder mechanical energy into thermal energy, but the reverse is too improbable to even consider as a possibility.
What we have been calling "non-conservative forces" are simply forces that can't help but bridge the macroscopic model to the microscopic. It's not a coincidence that when we first discussed friction, we took a brief detour into a microscopic model of irregularities of surfaces. Similarly, our first discussion of air drag included a diversion into a microscopic model of tiny particles bouncing off the affected object. The conservative force of gravity, on the other hand, acts on every particle in a macroscopic object at the same time, introducing no random differences between the fates of individual particles.
Energy Transfer
As we head back into our macroscopic model, it is useful to revise our notion of what work is. Up to now, we have thought about it as a way of isolating Newton's second law to changes in speed, in terms of the work-energy theorem. But an even more useful way to think about work is as a means by which energy is transferred. This transfer comes in one of three forms:
- Energy is transferred into or out of a system (through an external force)
- Energy is transferred from one mechanical form (KE or PE) into another mechanical form (through an internal conservative force).
- Energy is transferred from a mechanical form into thermal (through an internal non-conservative force).
When it comes to solving problems that involve calculating the energy transferred, in case #1 we generally have no choice but to calculate the work done directly, though a line integral. In case #2, we have the potential energy functions already cataloged, and we don't have to deal with a work calculation at all. But in case #3, there are multiple approaches that might arise. One might be a direct calculation (use the friction force and displacement to find the work done). Another might be simply to find what is "left over" – if the system is closed and the mechanical energy is not conserved, the remaining energy transferred must have gone into thermal energy.
Heat
It turns out that the three cases above do not exhaust the possible ways that energy can be transferred. Suppose we put our system "in contact with" (whatever that means) an external system that exerts no macroscopic force, so that no external work is done between the systems. It is nevertheless possible to transfer energy between the systems microscopically. That is, thermal energy can be transferred into or out of a system without any work being done through a direct interaction of the two systems' microscopic energy modes. This form of energy transfer is called heat.
Alert
A common misconception is that heat and thermal energy are the same thing. Heat is like work – it is a means for transferring energy, not the energy itself (though it has units of energy). That is, heat is not contained within a system like thermal energy is. If this is confusing, think of it this way: If one system transfers energy to another system mechanically, it doesn't "lose work" while the other system "gains work" – work is not stored within the systems. We know this because work comes from force, which is an interaction between systems. Heat is exactly analogous to work, in that it is not contained in systems, it is an accounting of the energy exchanged.
Since we now know a system can receive energy from outside by a mode other than external work, we need to include this mode in our energy model equation. It is standard to use the variable Q to represent heat, and this value is considered to be positive when energy is added to a system. Thus we have:
Q+Wext=ΔKE+ΔPE1+ΔPE2+⋯+ΔEthermal
This equation simply states that the amount of energy transferred into or out of the system microscopically (heat), plus the amount of energy transferred into or out of the system macroscopically (work) equals the amount that the energy within the system changes. This expression of overall energy conservation is known as the first law of thermodynamics (although usually when one studies the subject of thermodynamics, the mechanical energy terms are ignored).
Also note that heat can be transferred between objects within a system, and in this case the energy transfer is between ΔEthermal's for different objects within the system. Within the system we therefore have three modes of energy transfer from one type to another: (1) Work done by conservative forces converting between KE and PE, (2) Work done by non-conservative forces converting ME into thermal energy, (3) Heat transferred from one object to another raising the latter's thermal energy while reducing the former's.
We will not delve into the details of exactly how heat transfer occurs in this course, except to say that what enables it is a temperature difference between the two systems. When two systems at different temperatures exchange heat energy, it flows from the region of higher temperature to that of lower temperature, and this continues until both regions reach the same temperature (a condition that is referred to as thermal equilibrium).
Temperature Changes
Up to now, we have carefully avoided an aspect of thermal energy that arises naturally when the word "thermal" comes up. This form of energy must have something to do with temperature. Certainly it should come as no surprise that when a system's thermal energy rises, it gets hotter. Indeed, everyone has had experience with work done by kinetic friction causing the temperature of the objects to rise, such as rubbing one's hands together on a cold day.
What makes this interesting is that we can measure temperature changes, and relate these changes back to the amount of energy we know has been transferred. Rather than leap back into the realm of the microscopic to deal with this topic theoretically (we'll leave this to the aforementioned future course), we'll take an experimental approach to this. Suppose we move some energy into an object by the means of heat transfer. This energy can be moved from outside the system or within it. The question is, how is the amount of energy transferred into or out of an object related to that object's temperature change?
- We find that if we move twice as much energy into the object, its temperature rises twice as much. This tells us that the temperature change is proportional to the energy transferred:
Q∼ΔT
Alert
Note that the heat transferred is negative if the object drops in temperature (ΔT<0), so we define heat as positive when it transfers into an object, and negative when it transfers out.
Note that the heat transferred is negative if the object drops in temperature (ΔT<0), so we define heat as positive when it transfers into an object, and negative when it transfers out.
- We find that if we double object's mass and repeat the experiment, then the temperature only changes half as much as before. This seems to indicate that how much the the transferred energy is spread out is important. Or put another way, temperature seems to measure the average amount of energy added (or taken away) per atom. If the same amount of energy is spread out across more atoms, then the temperature change is less. So we can now include the mass in our proportionality:
Q∼mΔT
- We find that if we change the type of material out of which the object is composed, then even with the same mass and same amount of energy transferred, the temperature change can be different. Characterizing the type of material with a constant c (called the specific heat capacity – a terrible name, actually), we finally get a full equation relating the energy transferred to the change in temperature:
The units of this constant involves measurement of temperature. In the SI units we are working with, temperature is measured in degrees centigrade (oC), so:
[c]=JkgoC
A very common alternative system of units used for energy in the context of specific heat capacity is calories. This is a convenient system because it is defined in terms of the temperature change of a specified amount of liquid water. To be precise, one calorie of energy is the amount that the thermal energy of one gram of liquid water must be increased in order to raise its temperature from 14.5oC to 15.5oC. That is a far more precise definition than we will require. For our purposes, the added energy that raises the temperature of one gram of water (at any starting temperature) by one degree centigrade is an adequate definition of a calorie. Notice that using calories as our unit for energy gives us a very easy-to-remember value for the specific heat capacity of water – it is simply: cliquidwater=1calgoC.
We can, of course, convert between calories and joules, and it turns out that:
1cal=4.184J⇒cliquidwater=4184JkgoC
Example 3.5.1
A 1.2kg block of lead at a temperature of 80oC is placed within an insulated container containing 0.6kg of water at a temperature of 20oC. The block warms the water as the water cools the lead, eventually bringing them both to a common temperature. Find this equilibrium temperature. The specific heat capacity of lead is 130JkgoC.
- Solution
-
When a system is "insulated," it means that it does not exchange energy via heat with the outside surroundings. This means that we can treat the lead + water as a single, closed system, which means that the total energy does not change. With the temperature of the lead falling, it is clearly losing thermal energy, as the increase in the water temperature means it is gaining thermal energy. This is a closed system in which there is clearly no external energy added or changes in mechanical energy, so we have:
Q+Wext=ΔKE+ΔPE+ΔEthermal⇒0=ΔEthermal(lead)+ΔEthermal(water)⇒ΔEthermal(lead)=−ΔEthermal(water)
The changes in these thermal energies are proportional to their temperature changes, and when they come to thermal equilibrium they end up with the same temperature, so plugging in Equation 3.5.5 for each case:
ΔEthermal(lead)=Q(leavinglead)=mLcLΔT=mLcL(T−80oC)ΔEthermal(water)=Q(enteringwater)=mWcWΔT=mWcW(T−20oC)}⇒T=mLcL(80o)+mWcW(20o)mLcL+mWcW=23.5o
Of course we know that work done by non-conservative forces like friction and air drag move energy from mechanical energy into the ΔEthermal category. This is not quite the same as when heat transfer does this (this requires a temperature difference), but it turns out that the relationship of temperature change with energy transferred in this way is the same, though one has to take care to properly distribute the energy between the objects rubbing against each other (or the object moving through a dragging fluid and the fluid itself).
Example 3.5.2
A 2600kg bronze statue is being moved across a marble floor at a speed of 1.5m/s on a pad that is effectively frictionless, when suddenly one of the movers accidentally steps on the pad and the statue slides off it, onto the slab of marble below, where it then slows to a stop due to kinetic friction. Assume the surfaces of the statue and floor exchange heat with each other as the slide occurs, so that the surfaces experience the same temperature change during the slide. Also assume that a very short time after the slide, the thermal energy has only distributed itself through a very thin layer of both surfaces, affecting only 2.0kg of the statue and 0.80kg of the floor. And finally, assume that during this short period, a negligible amount of heat is exchanged with the surroundings (i.e. the statue and marble slab may be treated as a closed system). Compute the temperature change of the affected thin layers of the statue and marble slab. The specific heat capacities of bronze and marble are 370JkgoC and 880JkgoC, respectively.
- Solution
-
The system starts with kinetic energy, which goes away, replaced with thermal energy. This happens by means of work done by kinetic friction, so this energy transfer can be treated in the same way as if it were transferred as heat. Using the same temperature change for both surfaces, we therefore have:
12mwholestatuev2=mstatuesurfacecbronzeΔT+mslabsurfacecmarbleΔT⇒ΔT=12mwholestatuev2mstatuesurfacecbronze+mslabsurfacecmarble=2.0oC
An interesting follow-up question is, "If the coefficient of friction between the statue and the floor is smaller (so that the statue slides farther), or larger (so the statue stops sooner), how does the answer change?" Well, the amount of KE lost is the same in every case, so the answer won't change. The different coefficient of friction changes the friction force, but the work it does is the same, because the change of displacement balances the change of force.
Phase Changes
Thermal energy consists of the microscopic kinetic and potential energies of the microscopic particles comprising an object. These particles are held together by forces that can be overcome if sufficient energy is added, causing (for example) rigidly-held particles in a solid to slide over each other freely, changing the phase of the substance to liquid. Even more added energy can disassociate the particles from each other entirely, allowing them to move totally freely as a gas. In both of these transitions, the added energy goes only into the phase change – it doesn't change the temperature of the sample.
Of course, these phase transitions can only occur at certain temperatures (pressures also play a role, which we will ignore here), known as the melting point [0oC for water] for the solid/liquid transition, and the boiling point [100oC for water] for the liquid/gas transition. When there is a change in thermal energy (which, as above, typically occurs as a result of heat transfer, though work done by kinetic friction again has the same effect), and this change causes a change in phase, the amount of mass that changes phase is proportional to the amount of energy transferred. We can express it this way:
Q=±L⋅δm,
where δm is the amount of mass that changes phase, and L is a constant that depends upon the specific substance and the type of phase change. The constant L is given another terrible name – it is called the latent heat, and obviously has units of J/kg. Because this quantity depends upon the type of phase transition, it is usually split into two types, one for each phase transition:
Q(melting/freezing)=±Lf⋅δm,Q(boiling/condensing)=±Lv⋅δm
The constant Lf is called the latent heat of fusion, and Lv is called the latent heat of vaporization. Note that the phase changes can go either way. The convention remains as before, that when heat enters the system, it is a positive value, and this will correspond to phase transitions from solid to liquid (melting) or liquid to gas (boiling). Negative values of heat correspond to energy leaving the system – phase transitions from liquid to solid (freezing), and gas to liquid (condensing).
Suppose we wanted to transition a very cold solid all the way to a very hot gas. There would be several steps involved:
- add energy to raise the solid's temperature to the melting point
- add energy to change the phase from solid to liquid (while not changing the temperature)
- add energy to raise the liquid's temperature to the boiling point
- add energy to change the phase from liquid to gas (while not changing the temperature)
- add energy to raise the gas's temperature
Every one of these steps involves a different constant. The specific heat capacities of the solid, liquid, and gaseous phases of the same substance are not the same, and the latent heat of fusion is not the same as the latent heat of vaporization for the same substance. This process is depicted in the graph in Figure 3.5.2.
Figure 3.5.2 – Effect of Heat Transfer on Temperature and Phase

[Note: In the final section of the graph, you'll note that there is an "n" in the equation relating heat and temperature change. This is because it is more common to measure the amount of a gas in a unit called "moles" rather than in units of mass. The heat capacity in this case is called "molar heat capacity," rather than specific heat capacity, as we are using for solid and liquid. This is all we will say about moles here, and will leave further discussion of this topic to a course in chemistry or a physics course in thermodynamics.]
Example 3.5.3
A 0.80kg block of ice at a temperature of −6.0oC is placed into a bucket containing 2.4kg of water that is at a temperature of 18oC. The water and ice are insulated from their surroundings, so they can only exchange heat with each other. Describe the state of the system when it comes to thermal equilibrium. Specifically, is the final state all ice, all water, or a mixture of both, and what is the temperature of the system? The specific heat capacity of ice is 2100JkgoC, and the latent heat of fusion for water is 330,000Jkg.
- Solution
-
These kinds of problems can be a bit tricky. We start by noting that energy is transferring (as heat) from the warmer water to the colder ice. As this happens, the water gets colder and the ice warmer. When one of them gets to the melting point, it will begin changing phase as the heat transfer continues, so we need to figure out which one reaches the melting point first. We do this by comparing the energy required to get each to the melting point:
Qice=micecice(+6.0o)=10,000J,Qwater=mwatercwater(−18o)=−180,000J
So clearly the ice gets to the melting point first. When it does, the water is still warmer than the melting point, so the heat transfer continues. Our next step is to determine if all the ice melts before the temperature of the water gets to the melting point. The amount of energy needed to melt all the ice (after it reaches the melting point) is:
Q=LfΔm=264,000J
But when the water loses 180,000J, it will be at the melting point, which means the heat transfer will cease (both the ice and water are at the same temperature), so it cannot give the ice enough energy to melt it all. Therefore the final state is a mix of ice and water, but how much of each? To determine this, we simply give all of the energy the water can give to the ice before the water reaches 0oC. Some of this energy warms the ice, and the rest melts some of it. The first 10,000J warms the ice to the melting point, so the remaining 170,000J does the melting:
Δm=QLf=0.52kg
So this leaves a final state containing 0.28kg of ice and 2.92kg of water, both at a temperature of 0oC.


