5.14: Mixed Dielectrics
- Page ID
- 6022
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This section addresses the question: If there are two or more dielectric media between the plates of a capacitor, with different permittivities, are the electric fields in the two media different, or are they the same? The answer depends on
- Whether by “electric field” you mean \(E\) or \(D\);
- The disposition of the media between the plates – i.e. whether the two dielectrics are in series or in parallel.
Let us first suppose that two media are in series (Figure \(V.\)16).
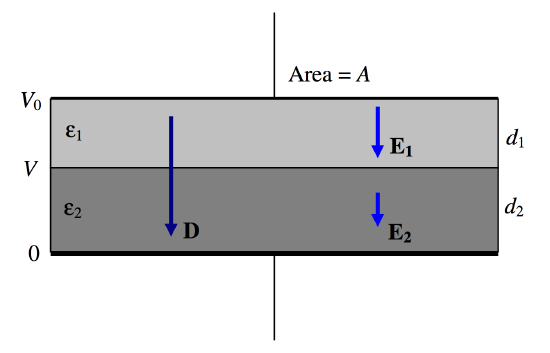
\(\text{FIGURE V.16}\)
Our capacitor has two dielectrics in series, the first one of thickness \(d_1\) and permittivity \(\epsilon_1\) and the second one of thickness \(d_2\) and permittivity \(\epsilon_2\). As always, the thicknesses of the dielectrics are supposed to be small so that the fields within them are uniform. This is effectively two capacitors in series, of capacitances \(\epsilon_1A/d_1 \text{ and }\epsilon_2A/d_2\). The total capacitance is therefore
\[C=\frac{\epsilon_1\epsilon_2A}{\epsilon_2d_1+\epsilon_1d_2}.\label{5.14.1}\]
Let us imagine that the potential difference across the plates is \(V_0\). Specifically, we’ll suppose the potential of the lower plate is zero and the potential of the upper plate is \(V_0\). The charge \(Q\) held by the capacitor (positive on one plate, negative on the other) is just given by \(Q = CV_0\), and hence the surface charge density \(\sigma\) is \(CV_0/A\). Gauss’s law is that the total \(D\)-flux arising from a charge is equal to the charge, so that in this geometry \(D = \sigma\), and this is not altered by the nature of the dielectric materials between the plates. Thus, in this capacitor, \(D = CV_0/A = Q/A\) in both media. Thus \(D\) is continuous across the boundary.
Then by application of \(D = \epsilon E\) to each of the media, we find that the \(E\)-fields in the two media are \(E_1\)=\(Q\)/\((\epsilon_1A\)) and \(E_2\)=\(Q\)/\((\epsilon_2A\)), the \(E\)-field (and hence the potential gradient) being larger in the medium with the smaller permittivity.
The potential V at the media boundary is given by \(V/d_2=E_2\). Combining this with our expression for \(E_2\), and \(Q = CV\)and Equation \ref{5.14.1}, we find for the boundary potential:
\[V=\frac{\epsilon_1d_2}{\epsilon_2d_1+\epsilon_1d_2}V_0.\label{5.14.2}\]
Let us now suppose that two media are in parallel (Figure \(V.\)17).
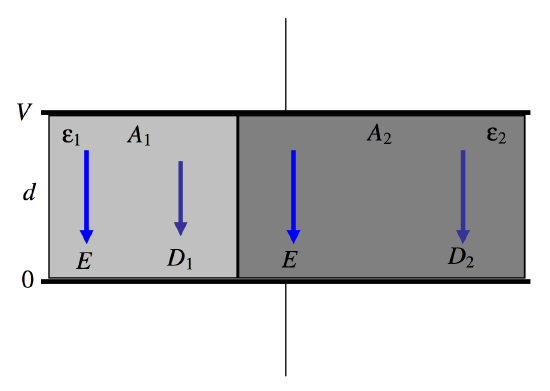
\(\text{FIGURE V.17}\)
This time, we have two dielectrics, each of thickness \(d\), but one has area \(A_1\) and permittivity \(\epsilon_1\) while the other has area \(A_2\) and permittivity \(\epsilon_2\). This is just two capacitors in parallel, and the total capacitance is
\[C=\frac{\epsilon_1A_1}{d}+\frac{\epsilon_2A_2}{d}\label{5.14.3}\]
The \(E\)-field is just the potential gradient, and this is independent of any medium between the plates, so that \(E = V/d\). in each of the two dielectrics. After that, we have simply that \(D_1=\epsilon_1E \text{ and }D_2=\epsilon_2E\). The charge density on the plates is given by Gauss’s law as \(\sigma = D\), so that, if \(\epsilon_1 < \epsilon_2\), the charge density on the left hand portion of each plate is less than on the right hand portion – although the potential is the same throughout each plate. (The surface of a metal is always an equipotential surface.) The two different charge densities on each plate is a result of the different polarizations of the two dielectrics – something that will be more readily understood a little later in this chapter when we deal with media polarization.
We have established that:
- The component of \(\textbf{D}\) perpendicular to a boundary is continuous;
- The component of \(\textbf{E}\) parallel to a boundary is continuous.
In Figure \(V.\)18 we are looking at the \(D\)-field and at the \(E\)-field as it crosses a boundary in which \(\epsilon_1 < \epsilon_2\). Note that \(D_y\) and \(E_x\)are the same on either side of the boundary. This results in:
\[\frac{\tan \theta_1}{\tan \theta_2}=\frac{\epsilon_1}{\epsilon_2}.\label{5.14.4}\]
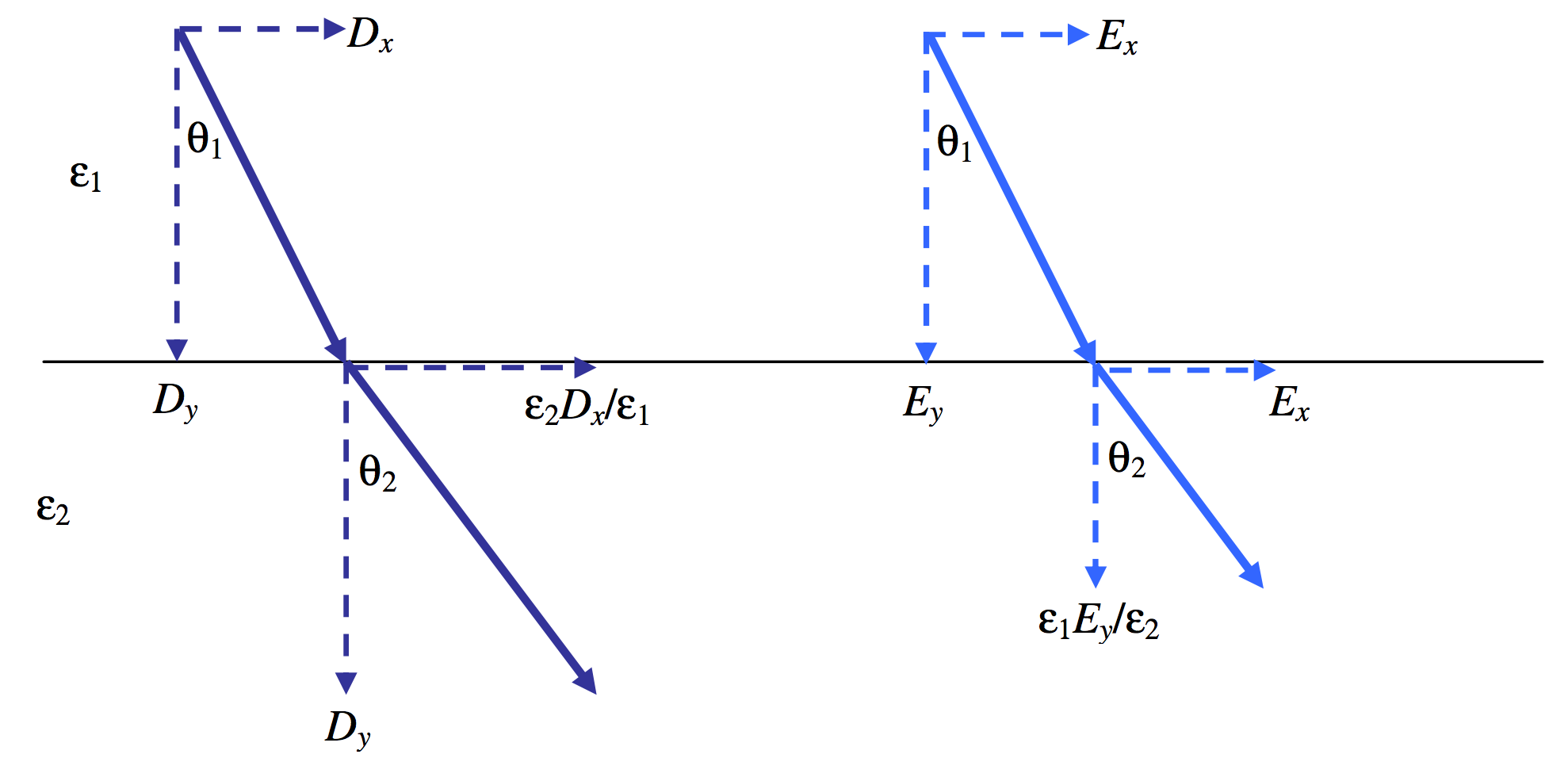
\(\text{FIGURE V.18}\)


