11.8: Problem

1. Show using the component form of the cross product given by equation (11.4) that A × B = -B × A.
2. A mass M is sliding on a frictionless table, but is attached to a string which passes through a hole in the center of the table as shown in figure 11.8. The string is gradually drawn in so the mass traces out a spiral pattern as shown in figure 11.8. The initial distance of the mass from the hole in the table is R and its initial tangential velocity is v. After the string is drawn in, the mass is a distance R′ from the hole and its tangential velocity is v′.
   1. Given R, v, and R′, find v′.
   2. Compute the change in the kinetic energy of the mass in going from radius R to radius R′.
   3. If the above change is non-zero, determine where the extra energy came from. 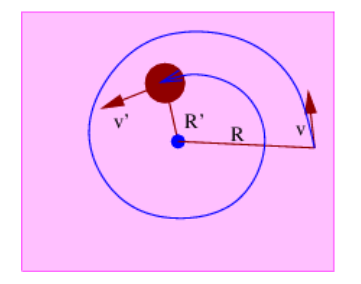Figure 11.8: Trajectory of a mass on a frictionless table attached to a string which passes through a hole in the table. The string is drawing the mass in.
3. A car of mass 1000 kg is heading north on a road at 30 m s^-1 which passes 2 km east of the center of town.
   1. Compute the angular momentum of the car about the center of town when the car is directly east of the town.
   2. Compute the angular momentum of the car about the center of town when it is 3 km north of the above point.
4. The apparatus illustrated in figure 11.9 is used to raise a bucket of mass M out of a well.
   1. What force F must be exerted to keep the bucket from falling back into the well?
   2. If the bucket is slowly raised a distance d, what work is done on the bucket by the rope attached to it?
   3. What work is done by the force F on the handle in the above case? 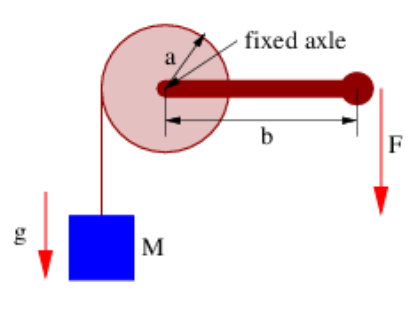Figure 11.9: A crank on a fixed axle turns a drum, thus winding the rope around the drum and raising the mass.
5. Derive equations below.
   1. \(K_{\text {total }}=K_{\text {trans }}+K_{\text {intern }}=\left[M_{\text {total }} V_{c m}^{2} / 2\right]+\left[M_{1} v_{1}^{\prime 2} / 2+M_{2} v_{2}^{\prime 2} / 2\right] \text { . }\)
   2. \(\mathbf{L}_{\text {total }}=\mathbf{L}_{\text {orb }}+\mathbf{L}_{\text {spin }}=\left[M_{\text {total }} \mathbf{R}_{c m} \times \mathbf{V}_{c m}\right]+\left[M_{1} \mathbf{r}_{1}^{\prime} \times \mathbf{v}_{1}^{\prime}+M_{2} \mathbf{r}_{2}^{\prime} \times \mathbf{v}_{2}^{\prime}\right]\)
6. A mass M is held up by the structure shown in figure 11.10. The support beam has negligible mass. Find the tension T in the diagonal wire. Hint: Compute the net torque on the support beam about point A due to the tension T and the weight of the mass M. 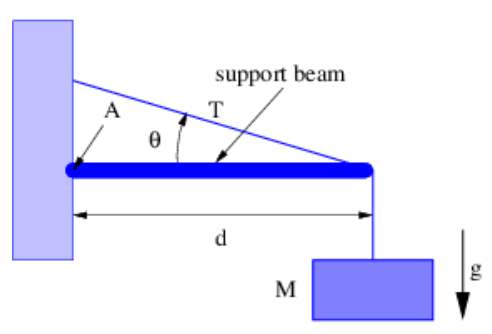Figure 11.10: A mass is supported by the tension in the diagonal wire. The support beam is free to pivot at point A.
7. A system consists of two stars, one of mass M moving with velocity v₁ = (0,v, 0) at position r₁ = (d, 0, 0), the other of mass 2M with zero velocity at the origin.
   1. Find the center of mass position and velocity of the system of two stars.
   2. Find the spin angular momentum of the system.
   3. Find the internal kinetic energy of the system. 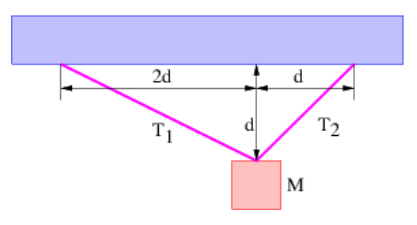Figure 11.11: A mass is supported by two strings. 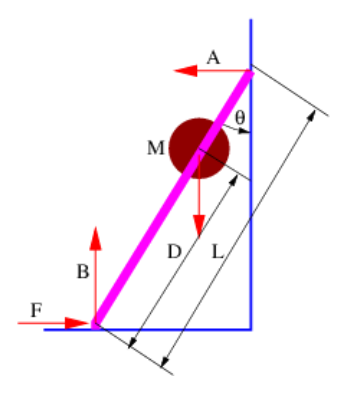Figure 11.12: A ladder leaning against a wall is held in place the force F acting on the base of the ladder.
8. A solid disk is rolling down a ramp tilted an angle θ from the horizontal. Compute the acceleration of the disk down the ramp and compare it with the acceleration of a block sliding down the ramp without friction.
9. A mass M is suspended from the ceiling by two strings as shown in figure 11.11. Find the tensions in the strings.
10. A man of mass M is a distance D up a ladder of length L which makes an angle \(\theta\) with respect to the vertical wall as shown in figure 11.12. Take the mass of the ladder to be negligible. Find the force F needed to keep the ladder from sliding if the wall and floor are frictionless and therefore can only exert normal forces A and B on the ladder.