10.8: Applications

Cameras

A camera which takes pictures can be explained using basic principles of geometric optics. The goal is to capture light coming from a physical object and project a de-magnified image of the object on a screen inside the camera. This can only be achieved by a converging lens that can create a real image on the screen. Here we model a camera as a hollow box with film or a detector on the back wall, which acts as our screen, where the image is detected. The lens has a fixed focal length \(f\), and is able to slide in and out of a tube in front of our box. While this is a rather simple model, it is sufficient to explain how most cameras (both film and digital) work.

Figure 10.8.1: Toy Model of a Camera

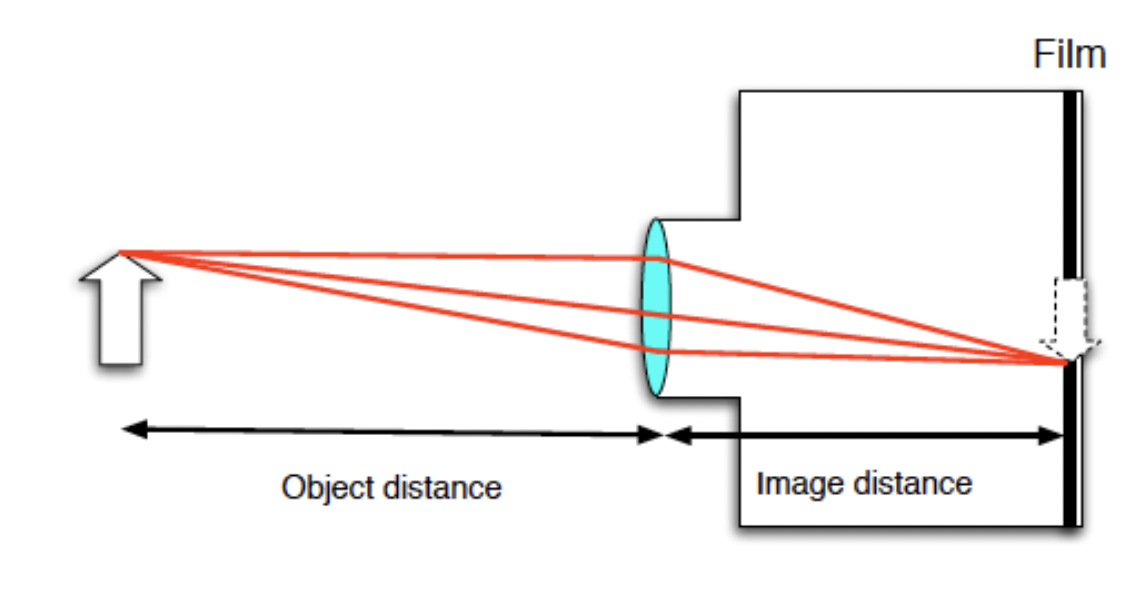
Note that since the camera lens produces a real image, it will appear upside-down on the film negative. This is taken into account in the film developing and printing process; this negative is used to project yet another real image onto the photograph print. This print is then right-side-up, unless your film developing service loads the negative into their processor incorrectly. If you have a Polaroid camera, which makes a direct print from exposure, the light from the lens must be flipped off of an internal mirror before exposing the Polaroid picture.

Since our simple camera has a lens of a fixed (positive) focal length \(f\), then the lens to image distance \(i\) must vary for different object distances \(o\), so that the image is in focus. In fact, if you inspect the thin lens equation, as the object distance \(o\) decreases (since \(f\) is fixed), then the image distance \(i\) must increase. You may have seen this for yourselves, as the lens barrel on your camera must be moved outwards to focus on close-up objects.

The Eye

The human eye processes images in a very similar manner as a camera. Light from an object refracts through the lens of our eye, and a real inverted image gets projected unto the retina in the back of the eye. Then the information travels through the optical nerve to our brain which interprets this image. A basic illustration of the anatomy of the eye is shown below. In contrast to a camera we cannot change the image distance significantly for our eye, since the length of the eye is fixed. 

Figure 10.8.2: Anatomy of an Eye

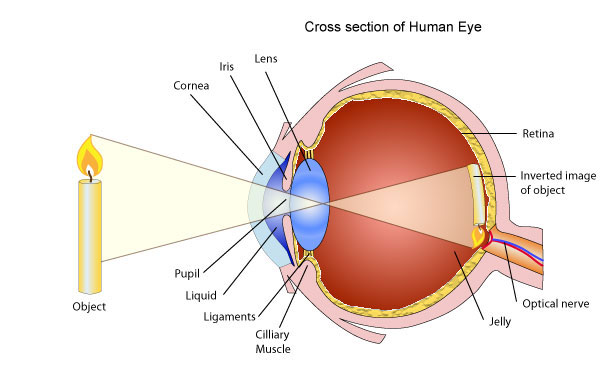
To get a focused image, the image distance \(i\) must be the same as the diameter of our eyeball. For most people this distance is roughly 2.5 cm. Because both the eye and a camera require focussing light onto a screen, they both require converging lenses. So if we cannot change \(i\) why can we see things in focus at a variety of distances? Unlike camera lenses, the lenses in our eyes can change focal length. We recall that a lens works by refraction, and while we cannot change the refractive index of our eye, the muscles around the eye, referred to as the ciliary muscles, can distort the lenses' shape, thus changing its focal length.

When the ciliary muscles are relaxed the lens is (relatively) flat, and the light rays are not bent much as they pass through. This results in a larger focal length, because it would take a long distance for light rays parallel to the optical axis to converge to a point. We relax our eyes when looking at distant objects, when our lens is at its longest focal length, \(f_{max}\). When the ciliary muscles contract, the lens becomes more round, and the normals change more. This corresponds to more bending of the light as it passes through the lens; the rounder lens has a smaller focal length. This minimal focal length is used when looking at near objects. Our ability to change the focal length of our eyes is referred to as accommodation.

There is a limit to how much the lenses in your eyes can change shape. Consequently there is a shortest focal length,\(f_{min}\), that your eyes can have, and a closest object that you can focus on clearly. The nearest distance that you can hold an object while still clearly focussing on it is called your near point, \(d_{np}\). Note that although it is called a "point" we actually refer to a distance. It is not the same as the shortest focal length, \(f_{min}\) rather they are related by:

\[\dfrac{1}{f_{min}} = \dfrac{1}{d_{np}} + \dfrac{1}{i}\]

In practice it is much easier to measure \(d_{np}\) than \(f_{min}\), because to measure \(d_{np}\) you only need to measure how close you can bring an object to your eye while still being able to focus on it. The nominal value for the near point of a middle-aged person is around 25 cm.

Similarly there is a furthest distance you can focus on when you totally relax your eyes. This distance is known as your far point, \(d_{fp}\). For “normal” healthy eyesight the far point is infinity – there is no furthest distance someone can focus on. However, if your eyes cannot relax completely, or your relaxed focal length is longer than your eyeball’s diameter, then you will have a far point. That is, you will not be able to focus on objects beyond some distance \(d_{fp}\). If your far point is at infinity, this means that the maximum focal length of a healthy eye is around the image distance, \(f_{max}\sim 2.5 cm\).

Corrective Lenses

Let us now consider three common defects of eyesight. Presbyopia (literally, “elderly eyes”) is nothing more than the normal loss of accommodation with advancing age. Children can read books much closer to their face than adults, because their near points are very short and their eyes are able to accommodate quite strongly. This ability decreases with age, so near points for children start to lengthen from as close as 10 cm, out to 25 cm by middle age (the nominal value for the near point), to even arm’s length or longer for older people. Typically, everyone will eventually develop presbyopia. When a presbyopic person’s near point is farther than 25 cm, glasses or contacts are prescribed to correct this vision defect.

Farsightedness (or hyperopia) is a condition where only far objects can be seen clearly. This is either because the lens cannot become round enough, or because the distance between the retina and the lens is too short. A farsighted person can see distant objects just fine with slight accomodation. As objects get closer, the eye must accommodate more strongly to focus images onto the retina. After a certain point, the eye cannot accommodate any further, and near objects remain out of focus.

Typically, children with hyperopic eyes will not have a problem with their vision, because they can strongly accommodate their eyes so they can see objects at any distance. However, as they gradually lose that ability as they grow up, then they will gradually not be able to see close-up objects. When a hyperopic person’s near point is farther than 25 cm, then glasses or contacts are prescribed to correct this vision defect.

Nearsightedness (or myopia) is the condition where only nearby things can be seen clearly. This is because the relaxed lens is too curved, or that the retina to lens distance is too long. Since the ciliary muscles can’t “unaccommodate” a lens and flatten it out, there is no way that a myopic eye can see distant objects. As a myopic person’s far point is closer than "infinity", then glasses or contacts are prescribed to correct this vision defect. However, while it is still relaxed, a myopic lens is able to focus on midrange objects. Accommodation easily allows the lens to focus on nearby objects.

When considering corrective lenses, we only need to worry about whether or not a (clear) final image can be made on the back of the retina. The way we go about this is by recalling that the eye itself is a lens, and responds the same to light that comes off an object directly and light that appears to be coming from the image of some object (as would be the case when we are wearing corrective lenses).

This gives us a strategy for modeling corrective lenses. We need to use a corrective lens because the object that we wish to focus on is closer than our near point or further away than our far point. The corrective lens creates an image of the object, and as we learned in our treatment of multiple lenses looking at the object through the corrective lenses is indistinguishable from trying to use our uncorrected eyesight to look at the image of the corrective lens. Provided the corrective lens places the image between our near point and our far point we will be able to see the object in question. By giving an object range that we wish to see (e.g. all objects up to 10 cm from my face) and knowing the near and far points, we can figure out what the focal length of the corrective lenses is required.

We can approximately model the required prescription (focal length) of the corrective lenses using the concepts introduced here. To correct presbyopia or hyperopia the corrective lens needs to make an image of the object at the near point of the patient's eye, when the object is at the near point of a healthy eye, \(o=25 \text{cm}\). For example, when reading you would like to hold the book at 25 cm, and your corrective lenses will make an image of the book at your near point where your eye can focus. The image has to be virtual since it needs to be created in front of the corrective lens. Also, since the image distance is further than the object distance, the lens must be converging. Neglecting the distance between the glasses and the eye, the focal length of the glasses is then:

\[\dfrac{1}{f_{lens}} = \dfrac{1}{0.25 \text{m}}-\dfrac{1}{d_{np}}\]

The object distance is written in meters due to units used for lenses in optometry, as described below. Assuming that near point is a positive distance, the minus sign in the equation above assures that the image distance is negative, since the image created is virtual.

For myopic eyes, the corrective lens needs to make an image of an object at "infinity", \(o=\infty\), at the far point of the patient where their eyes can focus. This lens must be diverging since the virtual image is closer to the lens than the object. Since \(1/\infty=0\), the focal length of the corrective lens (again neglecting the distance between the lens and the eye) is:

\[\dfrac{1}{f_{lens}} = -\dfrac{1}{d_{fp}}\]

As for the case of converging corrective lenses, the minus sign in the equation above assures that the image distance is negative since the image is virtual and the far point is a positive distance. This directly results in a negative focal length for the diverging lens being used to correct myopia.

Typically when people quote the “strength” of lenses the number quoted is not the focal length. Instead it is the number of optical strength, which is the inverse of the focal length, 1/f. The SI units of diopters (D) which is 1/meter. Thus, when converging a lens's focal length to diopters make sure the focal length is in units of meters.

Note this means that the less lens correction needed (which corresponds to less bending, and a higher focal length) corresponds to a lower number of diopters. Also note that depending on whether converging (\(f > 0\)) or diverging (\(f < 0\)) lenses are needed, the prescriptions for the lenses can be either a positive or negative number of diopters.

Example \(\PageIndex{1}\)

On a planet in a galaxy far, far away aliens have eyes with a “normal” length of 3.5cm.  An alien named Asil needs reading glasses, because her eyes are shorter than the "normal" length.  She was prescribed reading glasses with an optical power of 2.75D to correct her vision (so she can focus on objects as close as the aliens with “normal” eyes can). The lenses in Asil's eyes have the same minimum focal length, of 2.8cm, as that of "normal" eyes on her planet.

a) What is the closest distance a person with “normal vision” (on her planet) can focus on?  

b) Find the length of Asil’s eyes.

Solution

a) The minimum focal length, \(f_{\text{min}}\), of the eye is when an object is placed at the near point, \(o=N_{\text{normal}}\), and a real image is formed at a distance of the length of the eye, \(i=L_{\text{normal}}\):

\[\dfrac{1}{f_{\text{min}}}=\dfrac{1}{N_{\text{normal}}}+\dfrac{1}{L_{\text{normal}}}\nonumber\]

Solving for the near point of a healthy eye:

\[N_{\text{normal}}=\dfrac{1}{\dfrac{1}{2.8cm}-\dfrac{1}{3.5cm}}=14cm\nonumber\]

b) We can find Asil’s eye length by thinking that that when an object is at her near point, \(o=N_{\text{Asi}}\),  the image is at the length of her eye, \(i=L_{\text{Asil}}\), when her eye’s focal length is at its minimum:

\[\dfrac{1}{f_{\text{min}}}=\dfrac{1}{N_{\text{Asil}}}+\dfrac{1}{L_{\text{Asil}}}\nonumber\]

Solving for the length of the eye:

\[L_{\text{Asil}}=\dfrac{1}{\dfrac{1}{f_{\text{min}}}-\dfrac{1}{N_{\text{Asil}}}}\nonumber\]

To find Asil’s near point we use the equation for reading glass prescription: place object at the desired near point of 14cm (found in a) to create a virtual image at Asil’s near point: \(i=-N_{\text{Asil}}\):

\[\text{Optical Power}=2.25D=\dfrac{1}{N_{\text{normal}}}-\dfrac{1}{N_{\text{Asil}}}\nonumber\]

Solving for Asil's near point (we need to convert diopters to centimeters \(D=1/meter\):

\[N_{\text{Asil}}=\dfrac{1}{\dfrac{1}{14cm}-\dfrac{0.0275}{cm}}=22.8cm\nonumber\]

Finally, solving for the Asil's eye length using the first equation above:

\[L_{\text{Asil}}=\dfrac{1}{\dfrac{1}{2.8cm}-\dfrac{1}{22.8cm}}=3.19cm\nonumber\]

Asil's eye is shorter than a healthy eye length on this planet. This implies that light focuses behind Asil's eye and not on her retina, so she needs a converging corrective lens that would focus the light at a shorter distance, or on her retina. This is exactly why she needs reading glasses which contain converging lenses.