11.2: Introduction to Particle Physics
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the four fundamental forces and what particles participate in them
- Identify and describe fermions and bosons
- Identify and describe the quark and lepton families
- Distinguish between particles and antiparticles, and describe their interactions
Elementary particle physics is the study of fundamental particles and their interactions in nature. Those who study elementary particle physics—the particle physicists—differ from other physicists in the scale of the systems that they study. A particle physicist is not content to study the microscopic world of cells, molecules, atoms, or even atomic nuclei. They are interested in physical processes that occur at scales even smaller than atomic nuclei. At the same time, they engage the most profound mysteries in nature: How did the universe begin? What explains the pattern of masses in the universe? Why is there more matter than antimatter in the universe? Why are energy and momentum conserved? How will the universe evolve?
Four Fundamental Forces
An important step to answering these questions is to understand particles and their interactions. Particle interactions are expressed in terms of four fundamental forces. In order of decreasing strength, these forces are the strong nuclear force, the electromagnetic force, the weak nuclear force, and the gravitational force.
- Strong nuclear force. The strong nuclear force is a very strong attractive force that acts only over very short distances (about 10−15m). The strong nuclear force is responsible for binding protons and neutrons together in atomic nuclei. Not all particles participate in the strong nuclear force; for instance, electrons and neutrinos are not affected by it. As the name suggests, this force is much stronger than the other forces.
- Electromagnetic force. The electromagnetic force can act over very large distances (it has an infinite range) but is only 1/100 the strength of the strong nuclear force. Particles that interact through this force are said to have “charge.” In the classical theory of static electricity (Coulomb’s law), the electric force varies as the product of the charges of the interacting particles, and as the inverse square of the distances between them. In contrast to the strong force, the electromagnetic force can be attractive or repulsive (opposite charges attract and like charges repel). The magnetic force depends in a more complicated way on the charges and their motions. The unification of the electric and magnetic force into a single electromagnetic force (an achievement of James Clerk Maxwell) stands as one of the greatest intellectual achievements of the nineteenth century. This force is central to scientific models of atomic structure and molecular bonding.
- Weak nuclear force. The weak nuclear force acts over very short distances (10−15m) and, as its name suggest, is very weak. It is roughly 10−6 the strength of the strong nuclear force. This force is manifested most notably in decays of elementary particles and neutrino interactions. For example, the neutron can decay to a proton, electron, and electron neutrino through the weak force. The weak force is vitally important because it is essential for understanding stellar nucleosynthesis—the process that creates new atomic nuclei in the cores of stars.
- Gravitational force. Like the electromagnetic force, the gravitational force can act over infinitely large distances; however, it is only 10−38 as strong as the strong nuclear force. In Newton’s classical theory of gravity, the force of gravity varies as the product of the masses of the interacting particles and as the inverse square of the distance between them. This force is an attractive force that acts between all particles with mass. In modern theories of gravity, this force behavior is considered a special case for low-energy macroscopic interactions. Compared with the other forces of nature, gravity is by far the weakest.
The fundamental forces may not be truly “fundamental” but may actually be different aspects of the same force. Just as the electric and magnetic forces were unified into an electromagnetic force, physicists in the 1970s unified the electromagnetic force with the weak nuclear force into an electroweak force. Any scientific theory that attempts to unify the electroweak force and strong nuclear force is called a grand unified theory, and any theory that attempts to unify all four forces is called a theory of everything. We will return to the concept of unification later in this chapter.
Classifications of Elementary Particles
A large number of subatomic particles exist in nature. These particles can be classified in two ways: the property of spin and participation in the four fundamental forces. Recall that the spin of a particle is analogous to the rotation of a macroscopic object about its own axis. These types of classification are described separately below.
Classification by spin
Particles of matter can be divided into fermions and bosons. Fermions have half-integral spin (12ℏ,12ℏ,...) and bosons have integral spin (0ℏ,1ℏ,2ℏ,...).
Familiar examples of fermions are electrons, protons, and neutrons. A familiar example of a boson is a photon. Fermions and bosons behave very differently in groups. For example, when electrons are confined to a small region of space, Pauli’s exclusion principle states that no two electrons can occupy the same quantum-mechanical state. However, when photons are confined to a small region of space, there is no such limitation.
The behavior of fermions and bosons in groups can be understood in terms of the property of indistinguishability. Particles are said to be “indistinguishable” if they are identical to one another. For example, electrons are indistinguishable because every electron in the universe has exactly the same mass and spin as all other electrons—“when you’ve seen one electron, you’ve seen them all.” If you switch two indistinguishable particles in the same small region of space, the square of the wave function that describes this system and can be measured (|ψ|2) is unchanged. If this were not the case, we could tell whether or not the particles had been switched and the particle would not be truly indistinguishable. Fermions and bosons differ by whether the sign of the wave function (ψ) - not directly observable—flips:
ψ→−ψ(indistinguishablefermions),
ψ→+ψ(indistinguishablebosons).
Fermions are said to be “antisymmetric on exchange” and bosons are “symmetric on exchange.” Pauli’s exclusion principle is a consequence of exchange symmetry of fermions—a connection developed in a more advanced course in modern physics. The electronic structure of atoms is predicated on Pauli’s exclusion principle and is therefore directly related to the indistinguishability of electrons.
Classification by force interactions
Fermions can be further divided into quarks and leptons. The primary difference between these two types of particles is that quarks interact via the strong force and leptons do not. Quarks and leptons (as well as bosons to be discussed later) are organized in Figure 11.2.1. The upper two rows (first three columns in purple) contain six quarks. These quarks are arranged into two particle families: up, charm, and top (u, c, t), and down, strange, and bottom (d, s, b). Members of the same particle family share the same properties but differ in mass (given in MeV/c2). For example, the mass of the top quark is much greater than the charm quark, and the mass of the charm quark is much greater than the up quark. All quarks interact with one another through the strong nuclear force.
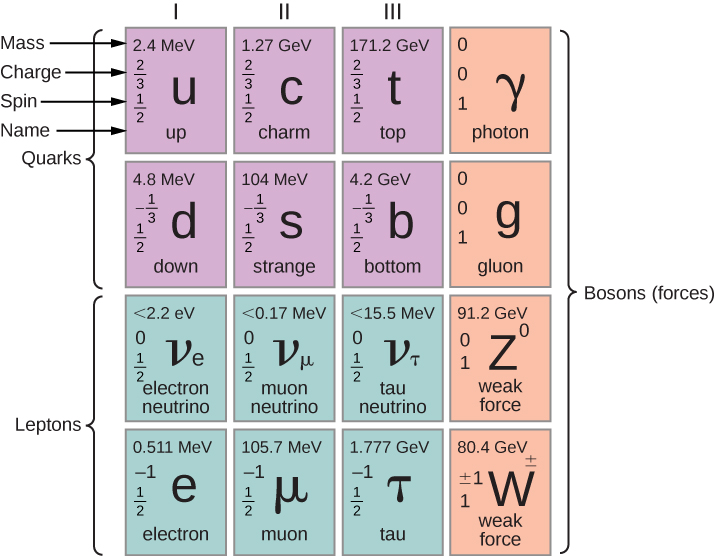
Ordinary matter consists of two types of quarks: the up quark (elementary charge, q=+2/3) and the down quark (q=−1/3). Heavier quarks are unstable and quickly decay to lighter ones via the weak force. Quarks bind together in groups of twos and threes called hadrons via the strong force. Hadrons that consist of two quarks are called mesons, and those that consist of three quarks are called baryons. Examples of mesons include the pion and kaon, and examples of baryons include the familiar proton and neutron. A proton is two up quarks and a down quark (p=uud,q=+1) and a neutron is one up quark and two down quarks (n=udd,q=0). Properties of sample mesons and baryons are given in Table 11.2.1. Quarks participate in all four fundamental forces: strong, weak, electromagnetic, and gravitational.
The lower two rows in the figure (in green) contain six leptons arranged into two particle families: electron, muon, and tau (e,μ,τ), and electron neutrino, muon neutrino, and tau neutrino (νe,νμ,νT).
The muon is over 200 times heavier than an electron, but is otherwise similar to the electron. The tau is about 3500 times heavier than the electron, but is otherwise similar to the muon and electron. Once created, the muon and tau quickly decay to lighter particles via the weak force. Leptons do not participate in the strong force. Quarks and leptons will be discussed later in this chapter. Leptons participate in the weak, electromagnetic, and gravitational forces, but do not participate in the strong force.
Bosons (shown in red) are the force carriers of the fermions. In this model, leptons and quarks interact with each other by sending and receiving bosons. For example, Coulombic interaction occurs when two positively charged particles send and receive (exchange) photons. The photons are said to “carry” the force between charged particles. Likewise, attraction between two quarks in an atomic nucleus occurs when two quarks send and receive gluons. Additional examples include W and Z bosons (which carry weak nuclear force) and gravitons (which carry gravitational force). The Higgs boson is a special particle: When it interacts with other particles, it endows them not with force but with mass. In other words, the Higgs boson helps to explains why particles have mass. These assertions are part of a tentative but very productive scientific model (the Standard Model) discussed later.
Particles and Antiparticles
In the late 1920s, the special theory of relativity and quantum mechanics were combined into a relativistic quantum theory of the electron. A surprising result of this theory was the prediction of two energy states for each electron: One is associated with the electron, and the other is associated with another particle with the same mass of an electron but with a charge of e+. This particle is called the antielectron or positron. The positron was discovered experimentally in the 1930s.
Soon it was discovered that for every particle in nature, there is a corresponding antiparticle. An antiparticle has the same mass and lifetime as its associated particle, and the opposite sign of electric charge. These particles are produced in high-energy reactions. Examples of high-energy particles include the antimuon (μ+), anti-up quark (u), and anti-down quark (d). (Note that antiparticles for quarks are designated with an over-bar.) Many mesons and baryons contain antiparticles. For example, the antiproton ((\overline{p}\)) is ¯u¯u¯d and the positively charged pion (π+) is u¯d. Some neutral particles, such as the photon and the π0 meson, are their own antiparticles. Sample particles, antiparticles, and their properties are listed in Table 11.2.1.
| Particle name | Symbol | Antiparticle | Mass (MeV/c2) | Average lifetime (s) | |
|---|---|---|---|---|---|
| Leptons | |||||
| Electron | e− | e+ | 0.511 | Stable | |
| Electron neutrino | νe | ¯νe | ≈0 | Stable | |
| Muon | μ− | μ+ | 105.7 | 2.20×10−6 | |
| Muon neutrino | νμ | ¯νμ | ≈0 | Stable | |
| Tau | τ− | τ+ | 1784 | <4×10−13 | |
| Tau neutrino | ντ | ¯ντ | ≈0 | Stable | |
| Hadrons | |||||
| Baryons | Proton | p | ¯p | 938.3 | Stable |
| Neutron | n | ¯n | 939.6 | 920 | |
| Lambda | Λ0 | ¯Λ0 | 1115.6 | 2.6×10−10 | |
| Sigma | ∑+ | ∑− | 1189.4 | 0.80×10−10 | |
| Xi | Ξ+ | Ξ− | 1315 | 2.9×10−10 | |
| Omega | Ω+ | Ω− | 1672 | 0.82×10−10 | |
| Mesons | Pion | π+ | π− | 139.6 | 2.60×10−8 |
| π-Zero | π0 | π0 | 135.0 | 0.83×10−16 | |
| Kaon | K+ | K− | 493.7 | 1.24×10−8 | |
| k-Short | K0S | ¯K0S | 497.6 | 0.89×10−10 | |
| k-Long | K0L | ¯K0L | 497.6 | 5.2×10−8 | |
| J/ψ | J/ψ | J/ψ | 3100 | 7.1×10−21 | |
| Upsilon | Υ | Υ | 9460 | 1.2×10−20 | |
Particles and their Properties
The same forces that hold ordinary matter together also hold antimatter together. Under the right conditions, it is possible to create antiatoms such as antihydrogen, antioxygen, and even antiwater. In antiatoms, positrons orbit a negatively charged nucleus of antiprotons and antineutrons. Figure 11.2.2 compares atoms and antiatoms.
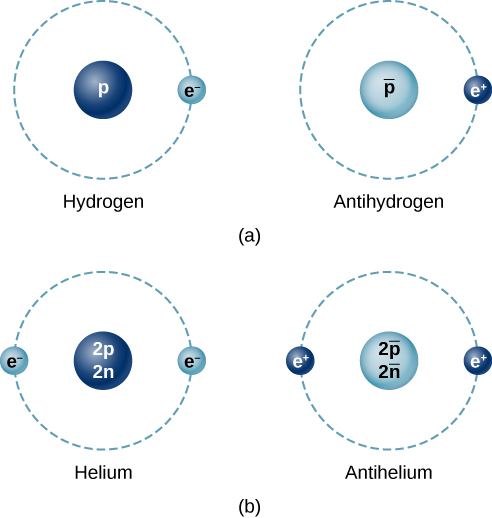
Antimatter cannot exist for long in nature because particles and antiparticles annihilate each other to produce high-energy radiation. A common example is electron-positron annihilation. This process proceeds by the reaction
e−+e+→2γ.
The electron and positron vanish completely and two photons are produced in their place. (It turns out that the production of a single photon would violate conservation of energy and momentum.) This reaction can also proceed in the reverse direction: Two photons can annihilate each other to produce an electron and positron pair. Or, a single photon can produce an electron-positron pair in the field of a nucleus, a process called pair production. Reactions of this kind are measured routinely in modern particle detectors. The existence of antiparticles in nature is not science fiction.
Watch this video to learn more about matter and antimatter particles.


