3.6: Exercise Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
3.1. Prove Eqs. (3)-(4), starting from Eq. (1.38) and Eq. (2) of this chapter.
3.2. A plane thin ring of radius R is charged with a constant linear density λ. Calculate the exact electrostatic potential distribution along the symmetry axis of the ring, and prove that at large distances, r>>R, the three leading terms of its multipole expansion are indeed correctly described by Eqs. (3)-(4).
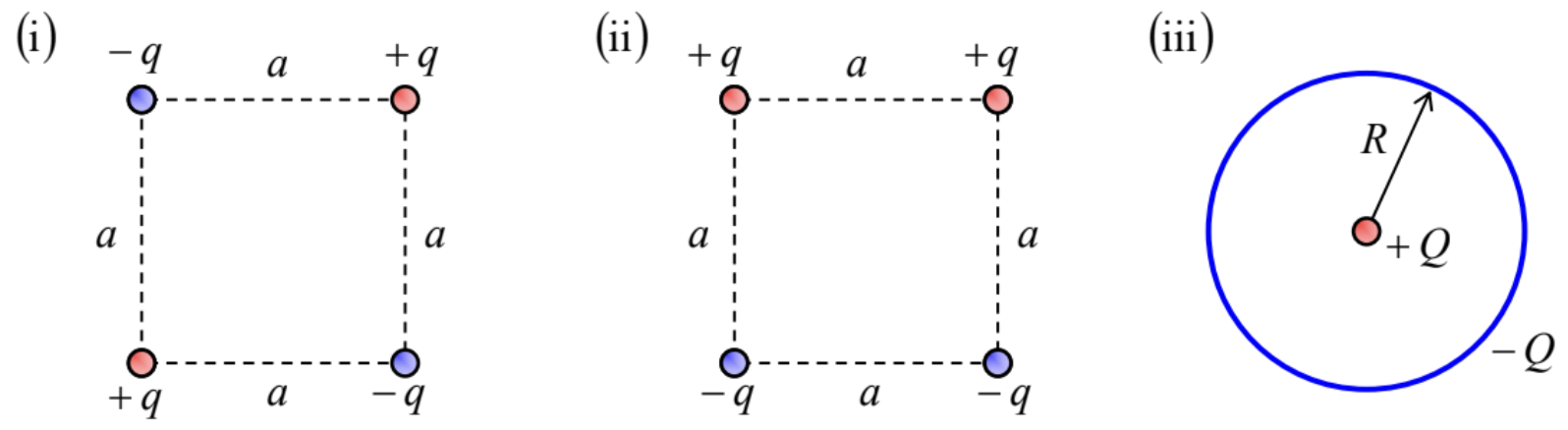
3.3. In suitable reference frames, calculate the dipole and quadrupole moments of the following systems (see Figs. below):
(i) four point charges of the same magnitude, but alternating signs, placed in the corners of a square;
(ii) a similar system, but with a pair charge sign alternation; and
(iii) a point charge in the center of a thin ring carrying a similar but opposite charge, uniformly distributed along its circumference.
3.4. Without carrying out an exact calculation, can you predict the spatial dependence of the interaction between various electric multipoles, including point charges (in this context, frequently called electric monopoles), dipoles, and quadrupoles? Based on these predictions, what is the functional dependence of the interaction between diatomic molecules such as H2, N2, O2, etc., on the distance between them, if the distance is much larger than the molecular size?
3.5. Two similar electric dipoles, of fixed magnitude p, located at a fixed distance r from each other, are free to change their directions. What stable equilibrium position(s) may they take as a result of their electrostatic interaction?
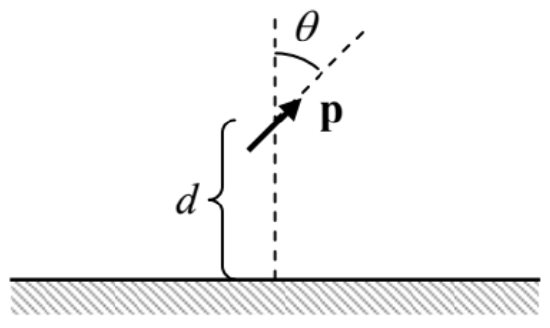
3.6. An electric dipole is located above an infinite, grounded conducting plane (see the figure on the right). Calculate:
(i) the distribution of the induced charge in the conductor,
(ii) the dipole-to-plane interaction energy, and
(ii) the force and the torque acting on the dipole.
3.7. Calculate the net charge Q induced in a grounded conducting sphere of radius R by a dipole p located at point r outside the sphere – see the figure on the right.

3.8. Use two different approaches to calculate the energy of interaction between a grounded conductor and an electric dipole p placed in the center of a spherical cavity of radius R, carved in the conductor.
3.9. A plane separating two parts of otherwise free space is densely and uniformly (with a constant areal density n) covered with electric dipoles, with similar moments p oriented in the direction normal to the plane.
(i) Calculate the boundary conditions for the electrostatic potential on both sides of the plane.
(ii) Use the result of Task (i) to calculate the potential distribution created in space by a spherical surface, with radius R, densely and uniformly covered with radially-oriented dipoles.
(iii) What condition should be imposed on the dipole density n for your results to be quantitatively valid?
3.10. Prove the Clausius-Mossotti relation (52) for the case of a cubic lattice of similar dipoles obeying Eq. (48): p=αEm, where Em is the microscopic electric field at the dipole’s location point.
Hint: Use Eq. (65) to account for the difference between the external field and the macroscopic field.
3.11. A sphere of radius R is made of a material with a uniform, fixed polarization P0.
(i) Calculate the electric field everywhere in space – both inside and outside the sphere.
(ii) Compare the result for the internal field with Eq. (24).
3.12. Calculate the electric field at the center of a cube with side a, made of a material with the uniform spontaneous polarization P0, directed parallel to one of the cube’s sides.
3.13. A stand-alone charge Q is distributed, in some way, in the volume of a body made of a uniform linear dielectric with a dielectric constant κ. Calculate the polarization charge Qef residing on the surface of the body, provided that it is surrounded by free space.
3.14. In two separate experiments, a thin plane sheet of a linear dielectric with κ=const is placed into a uniform external electric field E0:
(i) with sheet’s surface parallel to the electric field, and
(ii) the surface normal to the field.
For each case, find the electric field E, the electric displacement D, and the polarization P inside the dielectric (sufficiently far from the sheet’s edges).
3.15. A point charge q is located at distance r>>R from the center of a uniform sphere of radius R, made of a uniform linear dielectric. In the first nonzero approximation in small parameter R/r, calculate the interaction force, and the energy of interaction between the sphere and the charge.
3.16. A fixed dipole p is placed in the center of a spherical cavity of radius R, carved inside a uniform, linear dielectric. Calculate the electric field distribution everywhere in the system (both at r<R and at r>R).
Hint: You may start with the assumption that the field at r>R has a distribution typical for a dipole (but be ready for surprises :-).
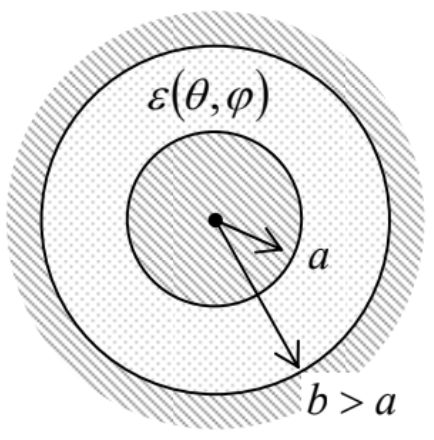
3.17. A spherical capacitor (see the figure on the right) is filled with a linear dielectric whose permittivity ε depends on spherical angles θ and φ, but not on the distance r from the system’s center. Derive an explicit expression for its capacitance C.
3.18. For each of the two capacitors shown in Fig. 10, calculate the electric forces (per unit area) exerted on the interface between the dielectrics, in terms of fields in the system.
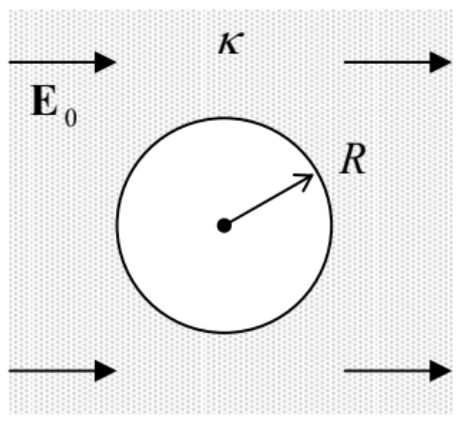
3.19. A uniform electric field E0 has been created (by distant external sources) inside a uniform linear dielectric. Find the change of the electric field, created by carving out a cavity in the shape of a round cylinder of radius R, with its axis normal to the external field – see the figure on the right.
3.20. Similar small spherical particles, made of a linear dielectric, are dispersed in free space with a low concentration n<<1/R3, where R is the particle's radius. Calculate the average dielectric constant of such a medium. Compare the result with the apparent but wrong answer
ˉκ−1=(κ−1)nV,(WRONG!)
(where κ is the dielectric constant of the particle's material and V=(4π/3)R3 is its volume), and explain the origin of the difference.
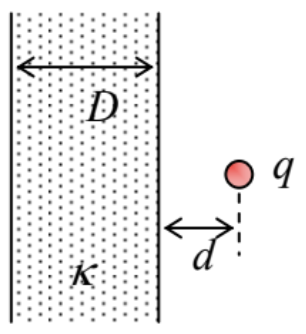
3.21.* Calculate the spatial distribution of the electrostatic potential induced by a point charge q placed at distance d from a very wide parallel plate, of thickness
D, made of a uniform linear dielectric – see the figure on the right.
3.22. Discuss the physical nature of Eq. (76). Apply your conclusions to a material with a fixed (field-independent) polarization P0, and calculate the electric field’s energy of a uniformly polarized sphere (see Problem 11).
3.23. Use Eqs. (73) and (82) to calculate the force of attraction of plane capacitor’s plates (per unit area), for two cases:
(i) the capacitor is charged to a voltage V, and then disconnected from the battery,31 and
(ii) the capacitor remains connected to the battery.
Reference
31 “Battery” is a common if misleading term for what is usually a single galvanic element. (The last term stems from the name of Luigi Galvani, a pioneer of electric current studies. Another term derived from his name is the galvanic connection, meaning a direct connection of two conductors, enabling a dc current flow – see the next chapter.) The term “battery” had to be, in all fairness, reserved for the connection of several galvanic elements in series – as was pioneered by L. Galvani’s friend Alexander Volta in 1800.


