11.4: Nuclear Reactions
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe and compare three types of nuclear radiation
- Use nuclear symbols to describe changes that occur during nuclear reactions
- Describe processes involved in the decay series of heavy elements
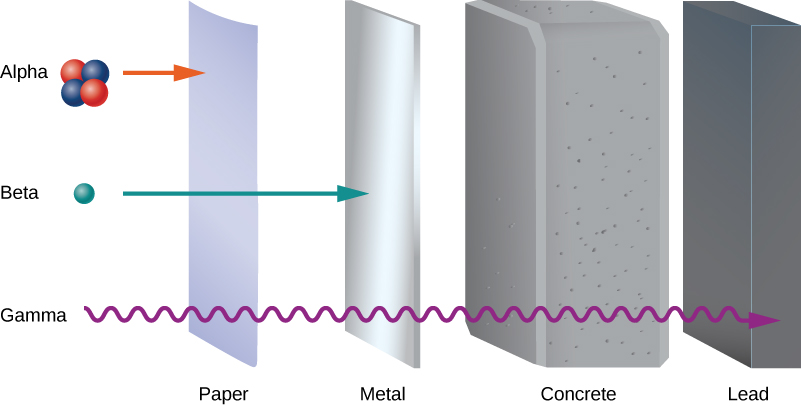
Early experiments revealed three types of nuclear “rays” or radiation: alpha (α) rays, beta (β) rays, and gamma (γ) rays. These three types of radiation are differentiated by their ability to penetrate matter. Alpha radiation is barely able to pass through a thin sheet of paper. Beta radiation can penetrate aluminum to a depth of about 3 mm, and gamma radiation can penetrate lead to a depth of 2 or more centimeters (Figure 11.4.1).
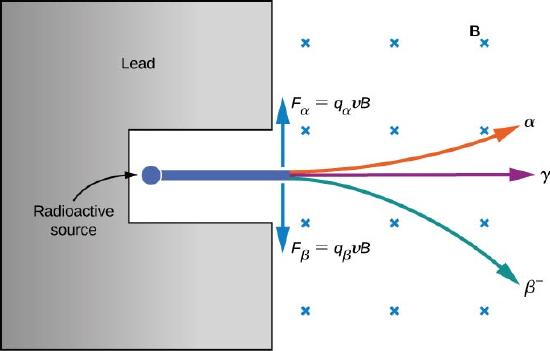
The electrical properties of these three types of radiation are investigated by passing them through a uniform magnetic field, as shown in Figure 11.4.2. According to the magnetic force equation for a moving charge in a magnetic field
→F=q→v×→B
where positively charged particles are deflected upward, negatively charged particles are deflected downward, and particles with no charge pass through the magnetic field undeflected. Eventually, α rays were identified with helium nuclei (4He), β rays with electrons and positrons (positively charged electrons or antielectrons), and γ rays with high-energy photons. We discuss alpha, beta, and gamma radiation in detail in the remainder of this section.
Alpha Decay
Heavy unstable nuclei emit α radiation. In α-particle decay (or alpha decay), the nucleus loses two protons and two neutrons, so the atomic number decreases by two, whereas its mass number decreases by four. Before the decay, the nucleus is called the parent nucleus. The nucleus or nuclei produced in the decay are referred to as the daughter nucleus or daughter nuclei. We represent an α decay symbolically by
ZAX→XZ−2A4−+He42
where AZX is the parent nucleus, A−4Z−2X is the daughter nucleus, and 42He is the α particle. In α decay, a nucleus of atomic number Z decays into a nucleus of atomic number Z−2 and atomic mass A−4. Interestingly, the dream of the ancient alchemists to turn other metals into gold is scientifically feasible through the alpha-decay process. The efforts of the alchemists failed because they relied on chemical interactions rather than nuclear interactions.
Watch alpha particles escape from a polonium nucleus, causing radioactive alpha decay. See how random decay times relate to the half-life. To try a simulation of alpha decay, visit alpha particles
An example of alpha decay is uranium-238:
U23892→X23490+He42
The atomic number has dropped from 92 to 90. The chemical element with Z=90 is thorium. Hence, Uranium-238 has decayed to Thorium-234 by the emission of an α particle, written
U23892→Th23490+He42
Subsequently, 23490Th decays by β emission with a half-life of 24 days. The energy released in this alpha decay takes the form of kinetic energies of the thorium and helium nuclei, although the kinetic energy of thorium is smaller than helium due to its heavier mass and smaller velocity.
Find the energy emitted in the α decay of 230Pu can be found using the equation E=(Δm)c2. We must first find Δm, the difference in mass between the parent nucleus and the products of the decay.
Solution
The decay equation is
Pu230→U235+He4.
Thus, the pertinent masses are those of 230Pu, 235U, and the α particle or 4He, all of which are known. The initial mass was m(230Pu)=230.052157u. The final mass is the sum
m(235U)+m(4He)=235⋅043924u+4⋅002602u
Thus,
Δm=m(230Pu)−[m(235U)+m(4He)]
=239.052157u−239.046526u
=0.0005631u.
Now we can find E by entering Δm into the equation:
E=(Δm)c2=(0.005631u)c2.
We know 1u=931.5MeV/c2, so we have
E=(0.005631)(931.5MeV/c2)(c2)=5.25MeV.
Significance
The energy released in this α decay is in the MeV range, many times greater than chemical reaction energies. Most of this energy becomes kinetic energy of the α particle (or 4He nucleus), which moves away at high speed. The energy carried away by the recoil of the 235U nucleus is much smaller due to its relatively large mass. The 235U nucleus can be left in an excited state to later emit photons (γ rays).239Pu→235U+4He.
Beta Decay
In most β particle decays (or beta decay), either an electron (β−) or positron (β+) is emitted by a nucleus. A positron has the same mass as the electron, but its charge is +e. For this reason, a positron is sometimes called an antielectron. How does β decay occur? A possible explanation is the electron (positron) is confined to the nucleus prior to the decay and somehow escapes. To obtain a rough estimate of the escape energy, consider a simplified model of an electron trapped in a box (or in the terminology of quantum mechanics, a one-dimensional square well) that has the width of a typical nucleus (10−14). According to the Heisenberg uncertainty principle in Quantum Mechanics, the uncertainty of the momentum of the electron is:
Δp≥hΔx=6.6×10−34m2⋅kg/s10−14m=6.6×10−20kg⋅m/s.
Taking this momentum value (an underestimate) to be the “true value,” the kinetic energy of the electron on escape is approximately
(Δp)22me=6.6×10−20m2⋅kg/s)22(9.1×10−31kg)=2.0×10−9J=12,400MeV.
Experimentally, the electrons emitted in β− decay are found to have kinetic energies of the order of only a few MeV. We therefore conclude that the electron is somehow produced in the decay rather than escaping the nucleus. Particle production (annihilation) is described by theories that combine quantum mechanics and relativity, a subject of a more advanced course in physics.
Nuclear beta decay involves the conversion of one nucleon into another. For example, a neutron can decay to a proton by the emission of an electron (β−) and a nearly massless particle called an antineutrino (¯ν):
n10→p11+e01+¯ν⋅
The notation 0−1e is used to designate the electron. Its mass number is 0 because it is not a nucleon, and its atomic number is −1 to signify that it has a charge of −e. The proton is represented by 11p because its mass number and atomic number are 1. When this occurs within an atomic nucleus, we have the following equation for beta decay:
zAX→AXZ+1+e01+¯ν⋅
This process occurs due to the weak nuclear force.
Watch beta decay occur for a collection of nuclei or for an individual nucleus.
As an example, the isotope 23490Th is unstable and decays by β− emission with a half-life of 24 days. Its decay can be represented as
Th23490→X23491+e+01+¯ν⋅
Since the chemical element with atomic number 91 is protactinium (Pa), we can write the β− decay of thorium as
Th23490→Pa23491+e+01+¯ν⋅
The reverse process is also possible: A proton can decay to a neutron by the emission of a positron (e+ and a nearly massless particle called a neutrino (v). This reaction is written as
p11→n10+e+01+ν⋅
The positron 01e is emitted with the neutrino ν, and the neutron remains in the nucleus. (Like β− decay, the positron does not precede the decay but is produced in the decay.) For an isolated proton, this process is impossible because the neutron is heavier than the proton. However, this process is possible within the nucleus because the proton can receive energy from other nucleons for the transition. As an example, the isotope of aluminum 2613Al decays by β+ emission with a half-life of 7.40×105y. The decay is written as
Al2613→X2612+e01+ν⋅
The atomic number 12 corresponds to magnesium. Hence,
Al2613→Mg2612+e01+ν⋅
As a nuclear reaction, positron emission can be written as
ZAX→AXZ−1+e01+ν⋅
The neutrino was not detected in the early experiments on β decay. However, the laws of energy and momentum seemed to require such a particle. Later, neutrinos were detected through their interactions with nuclei.
The _{83}^{211}Bi nucleus undergoes both \alpha and \beta^- decay. For each case, what is the daughter nucleus?
Strategy
We can use the processes described by Equation \ref{alpha} and Equation \ref{beta}, as well as the Periodic Table, to identify the resulting elements.
Solution
The atomic number and the mass number for the \alpha particle are 2 and 4, respectively. Thus, when a bismuth-211 nucleus emits an \alpha particle, the daughter nucleus has an atomic number of 81 and a mass number of 207. The element with an atomic number of 81 is thallium, so the decay is given by
\ce{_{83}^{211}Bi \rightarrow _{81}^{207} Ti + _2^4He.} \nonumber
In \beta^- decay, the atomic number increases by 1, while the mass number stays the same. The element with an atomic number of 84 is polonium, so the decay is given by
\ce{_{83}^{211}Bi \rightarrow _{84}^{211}Po + _{-1}^0e + \overline{\nu}.} \nonumber
In radioactive beta decay, does the atomic mass number, A, increase or decrease?
Solution
Neither; it stays the same.
Gamma Decay
A nucleus in an excited state can decay to a lower-level state by the emission of a “gamma-ray” photon, and this is known as gamma decay. This is analogous to de-excitation of an atomic electron. Gamma decay is represented symbolically by
\ce{_{Z}^{A}X}^{*} \ce{\rightarrow _{Z}^{A}X + \gamma} \label{gamma}
where the asterisk (*) on the nucleus indicates an excited state. In \gamma decay, neither the atomic number nor the mass number changes, so the type of nucleus does not change.
Radioactive Decay Series
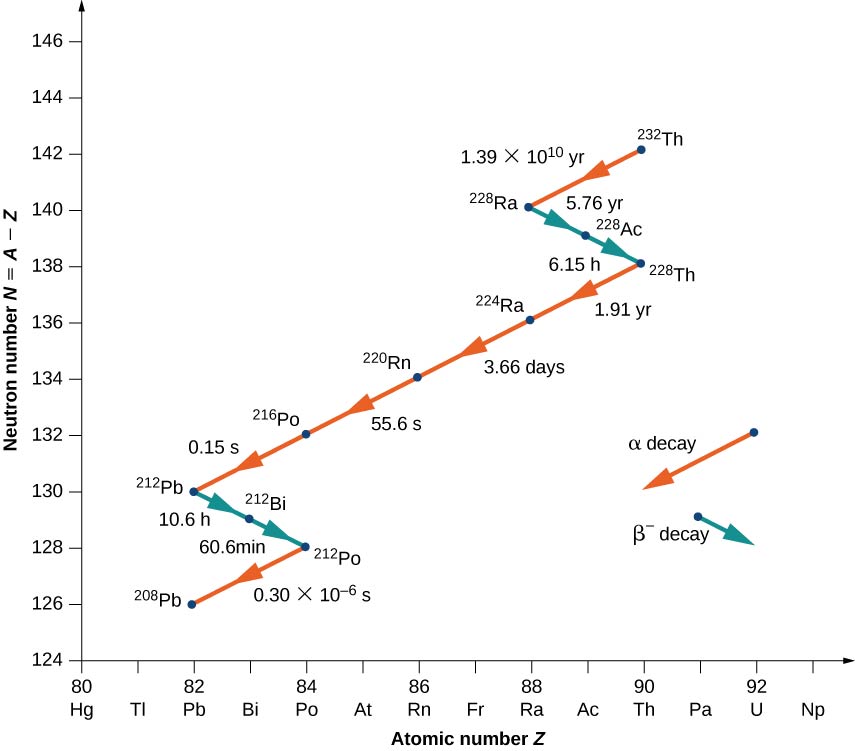
Nuclei with Z > 82 are unstable and decay naturally. Many of these nuclei have very short lifetimes, so they are not found in nature. Notable exceptions include _{90}^{232}Th (or Th-232) with a half-life of 1.39 \times 10^{10} years, and _{92}^{238}U (or U-238) with a half-life of 7.04 \times 10^8 years. When a heavy nucleus decays to a lighter one, the lighter daughter nucleus can become the parent nucleus for the next decay, and so on. This process can produce a long series of nuclear decays called a decay series. The series ends with a stable nucleus.
To illustrate the concept of a decay series, consider the decay of Th-232 series (Figure \PageIndex{3}). The neutron number, N, is plotted on the vertical y-axis, and the atomic number, Z, is plotted on the horizontal x-axis, so Th-232 is found at the coordinates (N, Z) = (142.90). Th-232 decays by \alpha emission with a half-life of 1.39 \times 10^{10} years. Alpha decay decreases the atomic number by 2 and the mass number by 4, so we have
\ce{_{90}^{232}Th \rightarrow _{88}^{228}Ra + _2^4He.} \nonumber
The neutron number for Radium-228 is 140, so it is found in the diagram at the coordinates (N,Z) = (140, \, 90). Radium-228 is also unstable and decays by \alpha emission with a half-life of 5.76 years to Actinum-228. The atomic number increases by 1, the mass number remains the same, and the neutron number decreases by 1. Notice that in the graph, α emission appears as a line sloping downward to the left, with both N and Z decreasing by 2. Beta emission, on the other hand, appears as a line sloping downward to the right with N decreasing by 1, and Z increasing by 1. After several additional alpha and beta decays, the series ends with the stable nucleus Pb-208.
The relative frequency of different types of radioactive decays (alpha, beta, and gamma) depends on many factors, including the strength of the forces involved and the number of ways a given reaction can occur without violating the conservation of energy and momentum. How often a radioactive decay occurs often depends on a sensitive balance of the strong and electromagnetic forces.
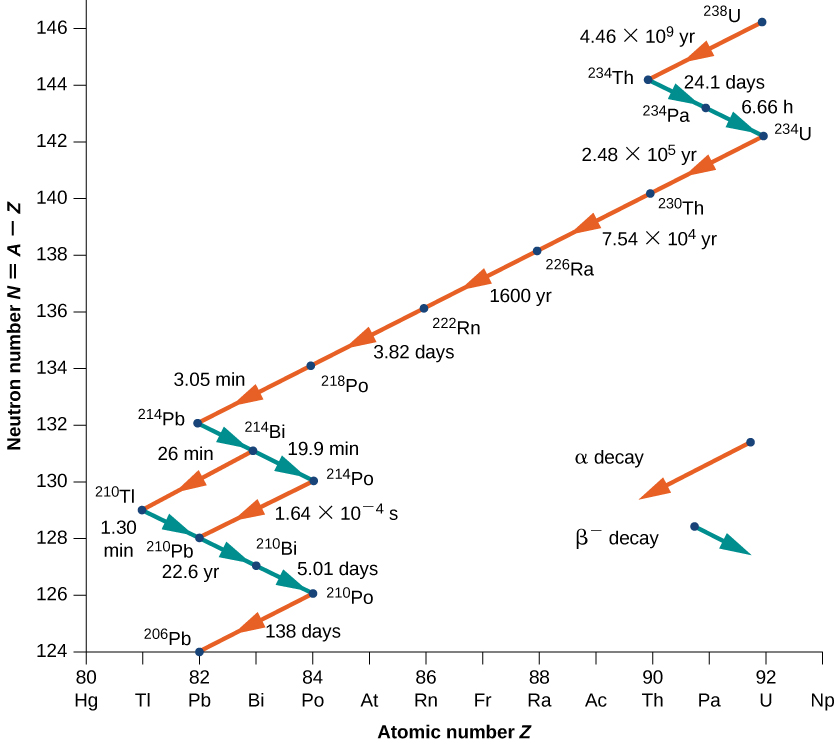
As another example, consider the U-238 decay series shown in Figure \PageIndex{4}. After numerous alpha and beta decays, the series ends with the stable nucleus Pb-206.
An example of a decay whose parent nucleus no longer exists naturally is shown in Figure \PageIndex{5}. It starts with Neptunium-237 and ends in the stable nucleus Bismuth-209. Neptunium is called a transuranic element because it lies beyond uranium in the periodic table. Uranium has the highest atomic number (Z + 92) of any element found in nature. Elements with Z > 92 can be produced only in the laboratory. They most probably also existed in nature at the time of the formation of Earth, but because of their relatively short lifetimes, they have completely decayed. There is nothing fundamentally different between naturally occurring and artificial elements.
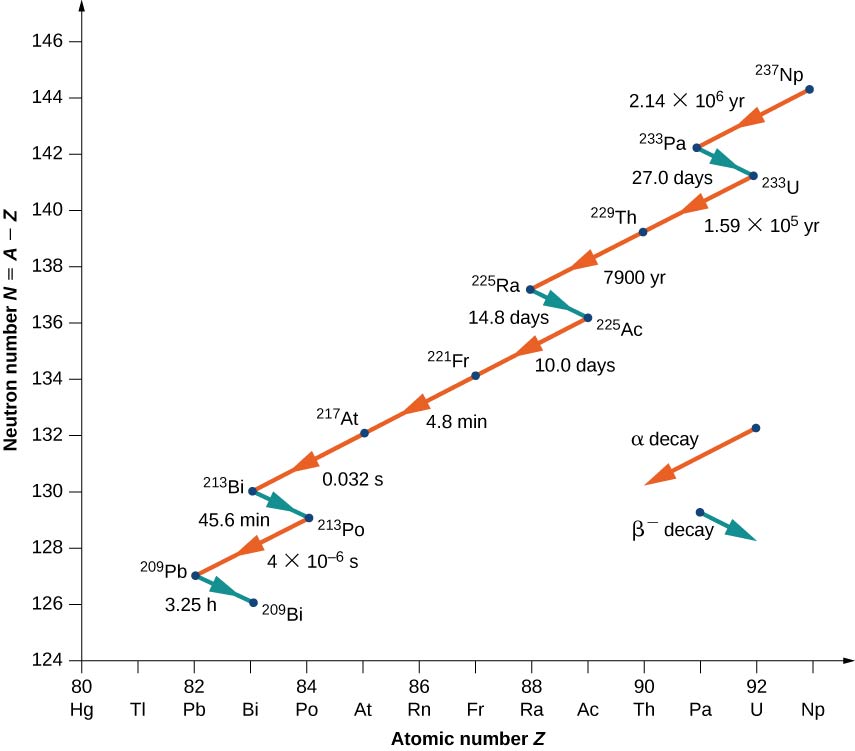
Notice that for Bi (21), the decay may proceed through either alpha or beta decay.
Radioactivity in the Earth
According to geologists, if there were no heat source, Earth should have cooled to its present temperature in no more than 1 billion years. Yet, Earth is more than 4 billion years old. Why is Earth cooling so slowly? The answer is nuclear radioactivity, that is, high-energy particles produced in radioactive decays heat Earth from the inside (Figure \PageIndex{6}).
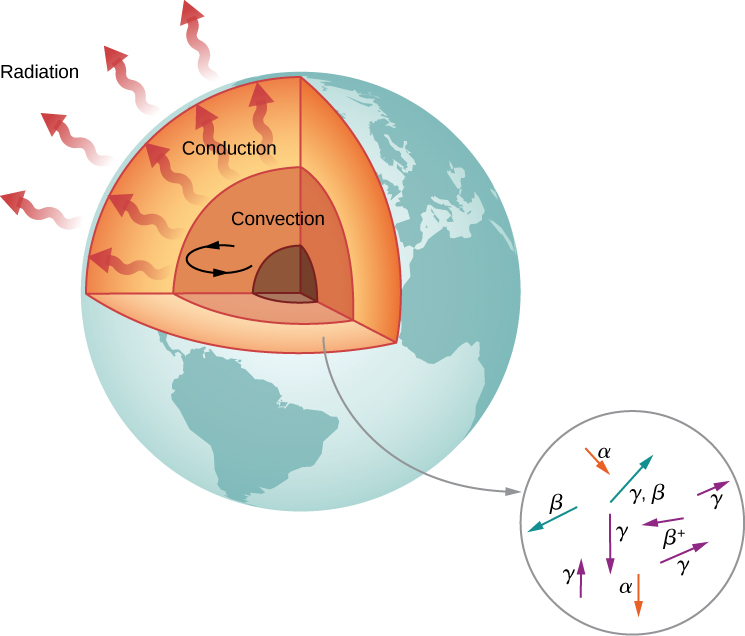
Candidate nuclei for this heating model are ^{238}U and ^{40}K, which possess half-lives similar to or longer than the age of Earth. The energy produced by these decays (per second per cubic meter) is small, but the energy cannot escape easily, so Earth’s core is very hot. Thermal energy in Earth’s core is transferred to Earth’s surface and away from it through the processes of convection, conduction, and radiation.


